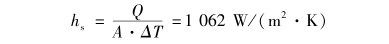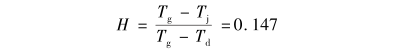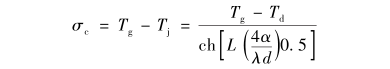短型熱電偶導(dǎo)熱誤差影響因素?cái)?shù)值仿真
發(fā)布時(shí)間:2022-10-31
瀏覽次數(shù):
摘要:在航空航天發(fā)動(dòng)機(jī)技術(shù)的研究過(guò)程中,通常需要準(zhǔn)確測(cè)量高溫,、高速環(huán)境下的氣流溫度以衡量發(fā)動(dòng)機(jī)的性能,由于傳感器強(qiáng)度等因素的限制,溫度傳感器插入高溫氣流深度較小,造成很大的導(dǎo)熱誤差,影響發(fā)動(dòng)機(jī)工作特性的評(píng)判,。對(duì)此專門開(kāi)展了
短型熱電偶溫度傳感器導(dǎo)熱誤差的研究,建立相應(yīng)的短型熱電偶導(dǎo)熱誤差仿真模型,并進(jìn)一步驗(yàn)證了仿真模型的準(zhǔn)確性,。在此基礎(chǔ)上通過(guò)仿真手段研究不同熱電偶插入深度,、不同來(lái)流馬赫數(shù),、不同來(lái)流總溫和不同基底溫度對(duì)導(dǎo)熱誤差修正系數(shù)的影響規(guī)律,并建立了熱電偶導(dǎo)熱誤差修正系數(shù)的響應(yīng)面模型,。仿真研究結(jié)果可以為短型熱電偶導(dǎo)熱誤差的抑制提供思路并為熱電偶使用過(guò)程中測(cè)量數(shù)據(jù)的修正提供支持,。
0引言
在先進(jìn)航空航天發(fā)動(dòng)機(jī)技術(shù)的研究中,經(jīng)常會(huì)遇到高溫,、高速氣流溫度測(cè)試問(wèn)題。例如:在液體火箭發(fā)動(dòng)機(jī)熱試車中,溫度參數(shù)的準(zhǔn)確測(cè)量對(duì)于衡量發(fā)動(dòng)機(jī)的性能是至關(guān)重要的,。由于熱電偶測(cè)溫方法具有造價(jià)低廉,、使用方便等特點(diǎn),目前在工程上廣泛采用,然而測(cè)溫?zé)犭娕纪ǔ9ぷ髟诟邷亍⒏邏焊咚倭鲃?dòng)環(huán)境下,熱電偶與燃?xì)?、周圍冷壁存在輻射換熱,并且沿偶絲向熱電偶?xì)んw存在熱傳導(dǎo)損失,電偶的指示值是熱電偶接點(diǎn)與周圍環(huán)境換熱形成的熱平衡溫度,并非測(cè)點(diǎn)處燃?xì)獾恼鎸?shí)溫度,。通常高溫測(cè)量誤差包含輻射誤差、導(dǎo)熱誤差以及速度誤差等,輻射誤差相對(duì)于導(dǎo)熱誤差而言所占份額較大,在研究過(guò)程中一般采用忽略導(dǎo)熱誤差的方法以簡(jiǎn)化計(jì)算,。然而在火箭發(fā)動(dòng)機(jī)的溫度測(cè)量過(guò)程中,,由于測(cè)溫傳感器強(qiáng)度等因素的限制,傳感器深入流道內(nèi)的尺寸很短,這樣會(huì)產(chǎn)生很大的導(dǎo)熱誤差,,而準(zhǔn)確評(píng)估導(dǎo)熱誤差的大小對(duì)發(fā)動(dòng)機(jī)的性能測(cè)量以及發(fā)動(dòng)機(jī)工作狀態(tài)的判定具有非常重要的意義,。
針對(duì)這一情況,溫度傳感器導(dǎo)熱誤差的數(shù)值仿真分析,研究在發(fā)動(dòng)機(jī)實(shí)際氣流速度條件下,溫度傳感器長(zhǎng)徑比以及支座溫度對(duì)導(dǎo)熱誤差的影響,獲得發(fā)動(dòng)機(jī)實(shí)際工況條件下短型熱電偶溫度傳感器導(dǎo)熱修正系數(shù),提高測(cè)量精度,。
1數(shù)值仿真方法及準(zhǔn)確性分析
1.1數(shù)值仿真方法
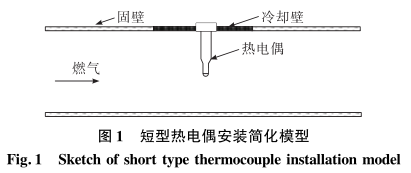
短型熱電偶采用鎧裝結(jié)構(gòu),熱電偶在流道安裝簡(jiǎn)化模型如圖1所示,為了消除輻射誤差的影響,流道壁溫設(shè)定與氣流溫度-致,流道壁厚2mm。n,。采用An-sys軟件進(jìn)行數(shù)值模擬,選用RNGK-ε湍流模型,標(biāo)準(zhǔn)壁面函數(shù)法,二階迎風(fēng)格式,、耦合隱式求解,氣流通道內(nèi)的速度和溫度壁面條件分別取壁面無(wú)滑移、等溫邊界條件,。氣流通道分別取壓力進(jìn)口和壓力出口,冷卻壁處溫度設(shè)置為測(cè)溫傳感器的冷端溫度,。流體區(qū)域和熱電偶?xì)んw固體區(qū)域采用熱固耦合。
1.2數(shù)值仿真方法準(zhǔn)確性分析
為了驗(yàn)證數(shù)值仿真的準(zhǔn)確性和可靠性,根據(jù).NACA研究報(bào)告中提供的氣流繞流熱電偶絲的導(dǎo)熱誤差相關(guān)試驗(yàn)數(shù)據(jù),在相同工況下采用Ansys軟件進(jìn)行仿真計(jì)算,并與文獻(xiàn)[2]中的導(dǎo)熱誤差修正系數(shù)對(duì)比來(lái)驗(yàn)證仿真結(jié)果的準(zhǔn)確性,。圖2為文獻(xiàn)[2]中的氣流繞流熱電偶絲示意圖,熱電偶絲總長(zhǎng)為L(zhǎng),L/2處為熱電偶接點(diǎn),基座處溫度為T,基座處溫度小于氣流溫度Tb<Tr,由于熱電偶絲向基座的導(dǎo)熱,,因此熱電偶接點(diǎn)處的溫度必定與氣流的溫度不一致,存在導(dǎo)熱誤差。表1為試驗(yàn)工況氣流參數(shù)和熱電偶絲幾何參數(shù),。
由表1中參數(shù)可得氣流雷諾數(shù)Re=3690,由文獻(xiàn)[2]中努賽爾數(shù)的計(jì)算方式:

為了校驗(yàn)數(shù)值仿真的準(zhǔn)確性,建立了氣流繞熱電偶絲的幾何模型,并采用Ansys軟件進(jìn)行相同工況下的導(dǎo)熱誤差仿真計(jì)算[12]
根據(jù)數(shù)值計(jì)算可得熱電偶表面平均換熱系數(shù)為:
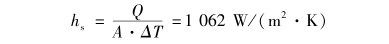
式中:Q為熱電偶絲向外部導(dǎo)熱量;A為電偶絲表面積;△T為流體與熱電偶絲的平均溫差,。這與從文獻(xiàn)[2]中得到的換熱系數(shù)917W/(m
22·K)非常接近。
另外提取仿真結(jié)果中熱電偶絲接點(diǎn)處的溫度.可得導(dǎo)熱誤差修正系數(shù):
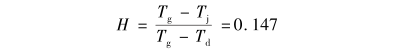
這與文獻(xiàn)[2]中查到此工況下的導(dǎo)熱修正系數(shù)0.16非常一致,。
上述計(jì)算結(jié)果表明,無(wú)論是熱電偶絲表面平均換熱系數(shù)還是熱電偶絲導(dǎo)熱誤差修正系數(shù),仿真結(jié)果與文獻(xiàn)[2]中的結(jié)果都非常一致,這也驗(yàn)證了數(shù)值仿真的準(zhǔn)確性,。
2數(shù)值模擬結(jié)果分析
熱電偶導(dǎo)熱誤差理論估算公式如[13]
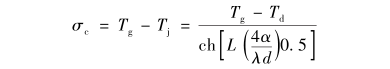
式中:Tg為氣流總溫;T;為熱電偶溫度示值;Td為支座溫度;α為熱電偶端與流體的對(duì)流換熱系數(shù);L為傳感器插人深度;d為傳感器直徑。
對(duì)于特定的熱電偶,λ和d已經(jīng)確定,,在測(cè)量中影響導(dǎo)熱誤差的主要因素有熱電偶插人深度,、對(duì)流換熱系數(shù)和支座溫度,而對(duì)流換熱系數(shù)主要受來(lái)流總溫和速度影響。下面將通過(guò)數(shù)值仿真分別研究熱電偶插人深度,、來(lái)流總溫,、來(lái)流馬赫數(shù)以及基座溫度對(duì)熱電偶導(dǎo)熱誤差的影響。
2.1熱電偶插入深度對(duì)導(dǎo)熱誤差的影響
來(lái)流馬赫數(shù)為0.3,來(lái)流總溫分別為573K,673K,773K,873K,在此條件下分別研究熱電偶插人深度30mm,20mm和10mm情況下導(dǎo)熱誤差的變化,。
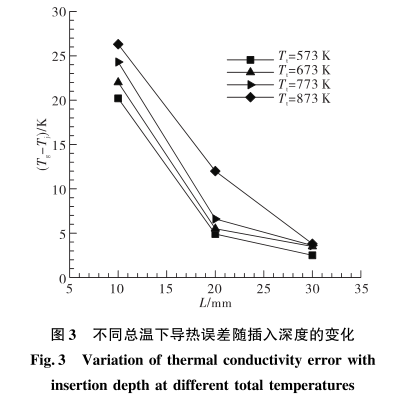
圖3給出了不同來(lái)流總溫條件下熱電偶導(dǎo)熱誤差隨插人深度的變化,可以看出,當(dāng)熱電偶插人深度為30mm時(shí),熱電偶導(dǎo)熱誤差約為4K,。隨著熱電偶插入深度的減小到20mm,導(dǎo)熱誤差增加到7K左右,但當(dāng)熱電偶插人深度減小到10mm時(shí),導(dǎo)熱誤差迅速增大到20~30K,這主要是由于熱電偶插人深度較短時(shí),熱電偶導(dǎo)熱熱阻減小使得導(dǎo)熱誤差增大.
2.2不同工況對(duì)熱電偶導(dǎo)熱誤差的影響研究

圖4為不同來(lái)流馬赫數(shù)情況下導(dǎo)熱誤差隨總溫.的變化趨勢(shì),可以看到,不同的來(lái)流馬赫數(shù)情況下導(dǎo)熱誤差都表現(xiàn)出隨總溫升高而增大的趨勢(shì),這是由于總溫升高后,熱電偶?xì)んw導(dǎo)熱率增加使得導(dǎo)熱熱阻降低,導(dǎo)熱誤差增大,。在同一總溫下,,導(dǎo)熱誤差表現(xiàn)出隨馬赫數(shù)增大而減小的趨勢(shì),這是由于隨著馬赫數(shù)的增大,氣流的特征雷諾數(shù)增大,從而使氣體與熱電偶的對(duì)流換熱系數(shù)增大,由導(dǎo)熱誤差理論估算公式13]可知,熱電偶導(dǎo)熱誤差減小。
2.3不同基底溫度對(duì)熱電偶導(dǎo)熱誤差的影響研究
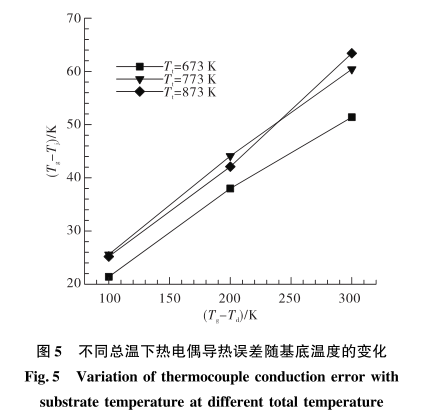
圖5為不同總溫下熱電偶導(dǎo)熱誤差隨Tg-Td的變化關(guān)系,,其中Tg-Td為氣流總溫與基底溫度的差值,Tg-Td越大表示基底溫度越低,。從圖5中可以看出,在不同的來(lái)流總溫情況下,熱電偶導(dǎo)熱誤差隨Tg-Td增大而增大,相同的Tg-Td情況下,氣流總溫越低熱電偶導(dǎo)熱誤差越小。
2.4導(dǎo)熱誤差修正系數(shù)數(shù)學(xué)模型
從以上熱電偶導(dǎo)熱誤差的仿真結(jié)果中可以看到,不同熱電偶插入深度,、氣流馬赫數(shù),、氣流總溫以及基底溫度都會(huì)對(duì)熱電偶導(dǎo)熱誤差產(chǎn)生影響。為了綜合分析各因素對(duì)導(dǎo)熱誤差修正系數(shù)的影響程度,根據(jù)上述計(jì)算中不同工況下導(dǎo)熱誤差的結(jié)果,,建立導(dǎo)熱誤差修正系數(shù)與熱電偶插人深度,、氣流總溫、氣流馬赫數(shù)和基底溫度的響應(yīng)面模型。
假設(shè)導(dǎo)熱誤差修正系數(shù)模型為二階響應(yīng)面模型,,并且不考慮交叉項(xiàng)的影響,。影響導(dǎo)熱誤差修正系數(shù)的因素分別為熱電偶插人深度L,氣流馬赫數(shù)Ma,氣流總溫T,以及總溫與基底的溫差,Tg-Td,則導(dǎo)熱誤差修正系數(shù)響應(yīng)面模型的數(shù)學(xué)表達(dá)式為:
H=β0+β1L+β2Ma+β3Tt+β4(,Tg-Td)+β5L²+β6Ma
2+β7Tt
2+β8g(,Tg-Td)
2
上式中共有9個(gè)未知數(shù),分別為....β0....β8,根據(jù)上述計(jì)算結(jié)果擬合可得:
β=[0.5713,-0.03697,-0.6845,0.0001973,-0.0003827,0.0006808,0.7838,-2.9133x10
-8,4.1737x10
-7]
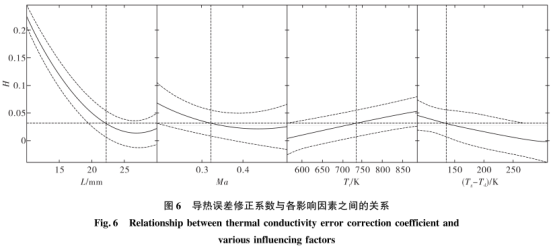
圖6為擬合得到的導(dǎo)熱誤差修正系數(shù)與各因素之間的關(guān)系,其中實(shí)線表示擬合曲線,而虛線為置信區(qū)間,可以看到,熱電偶插人深度對(duì)導(dǎo)熱誤差影響最大,,插入深度較小時(shí),導(dǎo)熱誤差很大,隨著熱電偶插人深度增加,導(dǎo)熱誤差迅速減小并趨于-一個(gè)很小的值,此情況下可認(rèn)為導(dǎo)熱誤差為零,因此在實(shí).際測(cè):量中應(yīng)選擇合適的熱電偶插人深度,減小測(cè)量誤差,。導(dǎo)熱誤差修正系數(shù)隨氣流馬赫數(shù)增大而減小,但其變化幅度較小并隨馬赫數(shù)增大而逐漸趨于平緩,。導(dǎo)熱誤差修正系數(shù)隨氣流總溫增加呈現(xiàn)近似線性增加,而導(dǎo)熱誤差隨Tg-Td的增大呈現(xiàn)近似線性的減小,,氣流溫度變化對(duì)誤差的影響主要原因是溫度變化造成了熱電偶?xì)んw平均熱導(dǎo)率的變化,從而使導(dǎo)熱熱阻發(fā)生變化,。
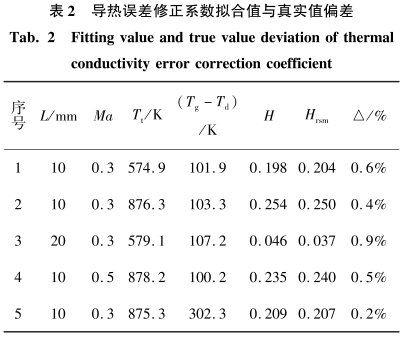
為了評(píng)估獲得的導(dǎo)熱誤差修正系數(shù)響應(yīng)面模型的準(zhǔn)確性,表2是不同工況下響應(yīng)面模型的計(jì)算值和真實(shí)值的比較,其中Hrsm是響應(yīng)面模型的計(jì)算值,H為相同工況下的真實(shí)值,,可以看到,二者之間差別非常小,這說(shuō)明建立的導(dǎo)熱誤差響應(yīng)面模型是準(zhǔn)確可信的,。
3結(jié)論
建立了短型熱電偶溫度傳感器導(dǎo)熱誤差仿真模型,通過(guò)與國(guó)內(nèi)數(shù)據(jù)對(duì)比驗(yàn)證了仿真模型的準(zhǔn)確性,。接著通過(guò)仿真計(jì)算,研究了不同熱電偶插入深度、不同來(lái)流馬赫數(shù),、不同來(lái)流總溫和不同基底溫度對(duì)導(dǎo)熱誤差修正系數(shù)的影響規(guī)律,,并建立了導(dǎo)熱誤差修.正系數(shù)的響應(yīng)面模型。主要有以下結(jié)論:
1)在熱電偶導(dǎo)熱誤差影響因素中,插人深度影響最大,。熱電偶導(dǎo)熱誤差隨插人深度減小迅速增大,當(dāng)熱電偶插人深度為30mm時(shí),熱電偶導(dǎo)熱誤差約為4K,。但當(dāng)熱電偶插人深度減小到10mm時(shí),導(dǎo)熱誤差迅速增大到20~30K。
2)相同的來(lái)流馬赫數(shù)情況下,,導(dǎo)熱誤差隨總溫升高而增大,這是由于總溫升高后,熱電偶?xì)んw導(dǎo)熱率增加使得導(dǎo)熱熱阻降低,導(dǎo)熱誤差增大,。在同一總溫下,導(dǎo)熱誤差表現(xiàn)出隨馬赫數(shù)增大而減小的趨勢(shì),這是由于隨著馬赫數(shù)的增大,氣流的特征雷諾數(shù)增大,從而使氣體與熱電偶的對(duì)流換熱系數(shù)增大,熱電偶導(dǎo)熱誤差減小,。
3)導(dǎo)熱誤差修正系數(shù)隨Tg-Td的增大而減小,,這種變化趨勢(shì)主要原因是當(dāng)Tg-Td增大時(shí),Td變小使得熱電偶?xì)んw的平均熱導(dǎo)率降低,導(dǎo)熱熱阻增加,從而使導(dǎo)熱誤差修正系數(shù)減小,。