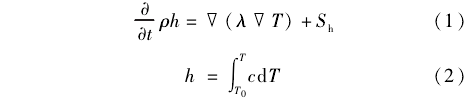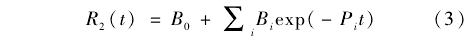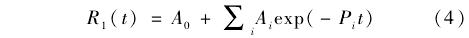鎧裝熱電偶動(dòng)態(tài)響應(yīng)校準(zhǔn)過程數(shù)值
發(fā)布時(shí)間:2023-06-08
瀏覽次數(shù):
摘要:時(shí)間常數(shù)是描述溫度傳感器動(dòng)態(tài)響應(yīng)特性的重要參數(shù),。由于實(shí)驗(yàn)室校準(zhǔn)條件通常難以覆蓋溫度傳感器的實(shí)際使用條件,因此基于有限體積法數(shù)值仿真插人法和回路電流階躍響應(yīng)(loopcurrentstepresponse,LCSR)法校準(zhǔn)
鎧裝熱電偶動(dòng)態(tài)響應(yīng)的過程,。建立了熱電偶保護(hù)管,、絕緣層,、感溫層的三維模型,分析了絕緣層MgO不同填充密實(shí)度下熱電偶的動(dòng)態(tài)響應(yīng),。結(jié)果發(fā)現(xiàn),采用3個(gè)極點(diǎn)的方程對(duì)LCSR響應(yīng)數(shù)據(jù)進(jìn)行擬合,、變換求得的時(shí)間常數(shù)與插入法獲得的時(shí)間常數(shù)偏差小于10%,為快響應(yīng)鎧裝熱電偶動(dòng)態(tài)特性的設(shè)計(jì),、校準(zhǔn)提供了一種新方法,。
1.引言
溫度傳感器的熱響應(yīng)時(shí)間描述其對(duì)階躍溫度的響應(yīng),對(duì)于可近似為一階系統(tǒng)的溫度傳感器,其輸出溫度變化達(dá)到階躍量的63.2%所需要的時(shí)間稱為時(shí)間常數(shù)。時(shí)間常數(shù)是影響動(dòng)態(tài)溫度測(cè)量準(zhǔn)確性的重要參數(shù),也是衡量溫度傳感器動(dòng)態(tài)響應(yīng)性能的重要指標(biāo),。由于影響時(shí)間常數(shù)的因素較多且復(fù)雜,通常需要實(shí)驗(yàn)來測(cè)量,。
溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)裝置包括:產(chǎn)生穩(wěn)定溫度場(chǎng)、速度場(chǎng)的恒溫恒速系統(tǒng),使溫度傳感器接受激勵(lì)的溫度階躍系統(tǒng),采集被校傳感器響應(yīng)信號(hào)的測(cè)試系統(tǒng),。時(shí)間常數(shù)是一個(gè)多影響量參數(shù),與傳感器的密度,、比熱容、導(dǎo)熱,、體積,、表面積以及傳感器與溫場(chǎng)介質(zhì)間的換熱系數(shù)等參數(shù)有關(guān)。傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)應(yīng)盡量與傳感器工作條件一致,。傳熱方式對(duì)溫度傳感器動(dòng)態(tài)特性的影響,采用油浴法和激光法對(duì)熱電偶時(shí)間常數(shù)進(jìn)行測(cè)試;在氣體溫度動(dòng)態(tài)校準(zhǔn)裝置中實(shí)驗(yàn)驗(yàn)證了一種
熱電偶級(jí)聯(lián)系統(tǒng)動(dòng)態(tài)性能評(píng)估方法;針對(duì)核電快響應(yīng)溫度計(jì),水流環(huán)境溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)裝置,并開展了不確定度評(píng)估;白鴿[7)對(duì)航空發(fā)動(dòng)機(jī)進(jìn)氣總溫傳感器開展了熱風(fēng)洞試驗(yàn),形成了某型傳感器的氣流馬赫數(shù)與響應(yīng)時(shí)間的關(guān)系曲線,。溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)的方法和裝置也用于動(dòng)態(tài)溫度測(cè)量誤差分析和不確定度評(píng)定。
溫度傳感器動(dòng)態(tài)響應(yīng)實(shí)驗(yàn)室校準(zhǔn)裝置通常難以實(shí)現(xiàn)與傳感器實(shí)際使用一致的條件,基于有限元或有限體積法的數(shù)值仿真技術(shù)逐步應(yīng)用在溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)中,,可模擬更寬的實(shí)驗(yàn)條件,節(jié)省大量實(shí)驗(yàn)時(shí)間和成本,。使用AnsysMechanical軟件模擬了光纖溫度傳感器在光脈沖加熱和溫度階躍輸人兩種情況下的時(shí)間常數(shù),結(jié)果均為ms級(jí);Luo等"采用有限元法分析了不同封裝材料(空氣、油脂,、銅)光纖溫度傳感器在正,、負(fù)溫度階躍激勵(lì)下的時(shí)間常數(shù);使用FloEFD軟件仿真分析了不同設(shè)計(jì)方案下鎳電阻溫度傳感器的動(dòng)態(tài)響應(yīng),優(yōu)選了填充材料、骨架材料、骨架形狀等參數(shù),。
回路電流階躍響應(yīng)(loopcurrentstepresponse,LCSR)法用于在役運(yùn)行條件下溫度計(jì)響應(yīng)時(shí)間的原位測(cè)量,。建立了LCSR法電阻溫度計(jì)響應(yīng)時(shí)間原位測(cè)量裝置,在裝置上驗(yàn)證了階躍電流和換熱條件對(duì)響應(yīng)時(shí)間的影響。
熱電偶因響應(yīng)快速而得到廣泛應(yīng)用,采用數(shù)值仿真技術(shù)鎧裝熱電偶的動(dòng)態(tài)響應(yīng)校準(zhǔn)過程,。首先建立了鎧裝熱電偶的三維結(jié)構(gòu)模型,進(jìn)行了網(wǎng)格劃分和網(wǎng)格無關(guān)解驗(yàn)證;其次分析了絕緣層MgO不同填充密實(shí)度下插人法和回路電流階躍法獲得的熱電偶動(dòng)態(tài)響應(yīng)曲線,對(duì)LCSR法響應(yīng)數(shù)據(jù)進(jìn)行擬合,、變換分析,比較了2種校準(zhǔn)方法獲得時(shí)間常數(shù)的偏差。
2熱電偶結(jié)構(gòu)與網(wǎng)格劃分
圖1為鎧裝熱電偶的剖面結(jié)構(gòu)圖,熱電偶的直徑設(shè)為D,鎧裝套管的壁厚設(shè)為0.1D,。為方便計(jì)算,設(shè)置正負(fù)極偶絲的直徑相同,均為0.2D,。
圖2為鎧裝熱電偶三維網(wǎng)格劃分示意圖,由于測(cè)量端的結(jié)構(gòu)復(fù)雜,采用適應(yīng)性良好的四面體網(wǎng)格劃分;電纜延伸段為規(guī)則的柱體,采用規(guī)則六面體網(wǎng)格劃分,以減少網(wǎng)格數(shù)量、節(jié)省計(jì)算時(shí)間,。取D=6mm進(jìn)行計(jì)算,。

3實(shí)驗(yàn)設(shè)計(jì)
以
K型鎧裝熱電偶為例,保護(hù)管為SUS304不銹鋼,絕緣層填充MgO粉,熱電極為鎳鉻/鎳硅合金,300K時(shí)材料的熱物性參數(shù)見表1熱電偶.絲焊接點(diǎn)近似為正極Ni-Cr10材料,以焊接點(diǎn)的平均溫度作為熱電偶輸出溫度,。

換熱系數(shù)是影響溫度傳感器熱響應(yīng)時(shí)間的重要參數(shù),。在擲人法溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)過程中,模擬環(huán)境溫度為300K,階躍溫度為50K,該過程可認(rèn)為是橫向流動(dòng)中圓柱體的強(qiáng)制對(duì)流換熱,根據(jù)Zukauskas關(guān)系式[15],以階躍過程的中間溫度325K作為熱電偶的等效溫度,計(jì)算得到水流速1m/s下的對(duì)流換熱系數(shù)為11851W/(m
2·K)。在LCSR法中,電流通過熱電偶絲產(chǎn)生焦耳熱,熱電偶焊接點(diǎn)溫度升高,通過對(duì)測(cè)得的溫度響應(yīng)數(shù)據(jù)擬合,、變換以計(jì)算時(shí)間常數(shù),。對(duì)熱電偶焊接點(diǎn)施加熱功率0.09W,能量密度為7.0x10
6W/m
3,焊接點(diǎn)產(chǎn)生的溫升小于0.5K,模擬LCSR法溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)過程,計(jì)算得到水流速1m/s時(shí)對(duì)流換熱系數(shù)為13101W/(m
2·K)。
絕緣層MgO粉填充的密實(shí)程度對(duì)絕緣層的密度,、比熱容和熱導(dǎo)率產(chǎn)生影響,進(jìn)而影響熱電偶的時(shí)間常數(shù),。絕緣層的密度為MgO粉和空氣密度的加權(quán)算數(shù)平均值,加權(quán)系數(shù)為MgO粉和空氣的體積百分?jǐn)?shù),MgO粉的體積百分?jǐn)?shù)定義為填充密實(shí)度r,。MgO粉的比熱容值0.924kJ/(kg·K)與空氣101.325kPa下的定壓比熱容值1.0066kJ/(kg·K)較接近,絕緣層的比熱容值按照MgO粉和空氣的體積百分?jǐn)?shù)加權(quán)算數(shù)平均的方法計(jì)算,。絕緣層屬于固相和氣相混合而成的兩相材料,其熱導(dǎo)率不僅與組成相的熱導(dǎo)率、相對(duì)體積分?jǐn)?shù),還與每相的分布,、排列,、取向有關(guān)。對(duì)于固相顆粒分散在流體中的情形,復(fù)合熱導(dǎo)率可用Maxwell公式[14]近似計(jì)算不同填充密實(shí)度r下絕緣層的熱物性參數(shù)如表2所示,。

4數(shù)學(xué)模型和網(wǎng)格,、浸沒深度驗(yàn)證
基于有限體積法進(jìn)行鎧裝熱電偶區(qū)域離散化,采用二階迎風(fēng)格式對(duì)能量方程進(jìn)行離散,采用基于單元格的最小二乘法差值對(duì)梯度方程進(jìn)行離散??刂品匠痰碾x散和求解為通用設(shè)置,不再贅述,。數(shù)值仿真在計(jì)算流體力學(xué)軟件Fluent中進(jìn)行。
模型的能量方程不涉及對(duì)流和輻射傳熱,,僅求解導(dǎo)熱形式:
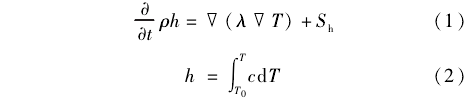
式中:h為離散單元體物質(zhì)的焓;λ為熱導(dǎo)率;c為比熱容;T0為參考溫度取298.15K;Sh表示熱源,在插人法中,Sh為0,在LCSR法中,Sh為向熱電偶施加的熱功率,。
基于三維瞬態(tài)算法求解模型,每時(shí)間步計(jì)算的能量方程殘差小于10
-8,總測(cè)試時(shí)間不少于20倍時(shí)間常數(shù)。采用可變時(shí)間步長(zhǎng),在階躍初期熱電偶焊接點(diǎn)溫度變化速率大,時(shí)間步長(zhǎng)為0.001s;在階躍后期熱電偶焊接點(diǎn)溫度變化速率小,逐漸接近水流溫度,時(shí)間步長(zhǎng)為0.05s,。
為選取合適的網(wǎng)格大小,,在保證計(jì)算精度的條件下節(jié)省計(jì)算時(shí)間,在水流速v=1m/s條件下,對(duì)擲人法溫度傳感器動(dòng)態(tài)響應(yīng)校準(zhǔn)過程進(jìn)行數(shù)值仿真,。分別以0.2、0.25,、0.3和0.35mm為主要尺寸對(duì)圖1所示的鎧裝熱電偶進(jìn)行網(wǎng)格劃分,,分別獲得444946、258867,、142484和96845個(gè)網(wǎng)格單元體,。

不同網(wǎng)格數(shù)量對(duì)熱電偶動(dòng)態(tài)響應(yīng)仿真結(jié)果的影.響如圖3所示,圖3(a)和圖3(b)分別為普通坐標(biāo)和對(duì)數(shù)坐標(biāo)下顯示的結(jié)果。由圖可知,4種網(wǎng)格數(shù)量下的溫度動(dòng)態(tài)響應(yīng)曲線幾乎完全重合,說明4種網(wǎng)格數(shù)量對(duì)熱電偶動(dòng)態(tài)響應(yīng)計(jì)算結(jié)果的影響不明顯,。為進(jìn)一步分析網(wǎng)格數(shù)量對(duì)數(shù)值仿真過程的影響,在時(shí)間0.5s時(shí)對(duì)比了z軸的溫度分布,如圖4所示,4種網(wǎng)格數(shù)量下的溫度分布曲線基本重合,。圖4中a、b,、c,、d4個(gè)區(qū)域分別對(duì)應(yīng)鎧裝熱電偶z軸上的不銹鋼保護(hù)管層、絕緣MgO層,、焊接點(diǎn)和絕緣MgO層,由圖可知,在每層交界附近,由于材料熱物性的突變,導(dǎo)致溫度曲線斜率存在明顯的變化,。基于圖3和圖4結(jié)果的分析,數(shù)值選用0.3mm為主要尺寸的網(wǎng)格劃分方式,,既能保證計(jì)算精度,又能節(jié)省計(jì)算時(shí)間,。

為消除熱電偶電纜延伸段軸向漏熱對(duì)測(cè)量結(jié)果的影響,,其末端橫截面設(shè)為絕熱壁面;并參照溫度傳感器允差校準(zhǔn)時(shí)對(duì)浸沒深度的要求,設(shè)置熱電偶的浸沒深度為15D,。開展了浸沒深度分別為5D、10D,、15D和20D條件下的數(shù)值仿真,結(jié)果顯示4種浸沒深度下溫度動(dòng)態(tài)響應(yīng)曲線幾乎完全重合,求得熱電偶的時(shí)間常數(shù)為0.627~0.630s,相對(duì)變化小于0.5%,說明邊界條件和浸沒深度設(shè)置合理,。
5結(jié)果分析與討論
插人法獲得的不同填充密實(shí)度r對(duì)熱電偶動(dòng)態(tài)響應(yīng)曲線的影響如圖5所示,圖中熱響應(yīng)曲線具有相似的形狀,隨著填充密實(shí)度的減小,熱電偶絕緣層的熱導(dǎo)率降低,導(dǎo)致溫度響應(yīng)曲線變緩,時(shí)間常數(shù)增大。圖6所示為r=0.996時(shí),,插人法和LCSR法獲得的熱電偶動(dòng)態(tài)響應(yīng)曲線,。為便于比較響應(yīng)曲線的變化,對(duì)溫度響應(yīng)數(shù)據(jù)進(jìn)行了歸一化處理。在局部放大圖中,由于熱電偶保護(hù)管和絕緣層的熱慣性,插人法獲得的溫度動(dòng)態(tài)響應(yīng)曲線在起始時(shí)刻后的一段時(shí)間內(nèi)變化不明顯,,該段時(shí)間稱為“延遲時(shí)間”(deadtime),。由于LCSR法直接使焊接點(diǎn)感溫層產(chǎn)生熱量,因而在起始階段不存在延遲時(shí)間。

將LCSR溫度響應(yīng)數(shù)據(jù)擬合到節(jié)點(diǎn)模型方程,,線然后對(duì)其作拉氏變換的反變換,可得出熱電偶對(duì)應(yīng)的模態(tài)響應(yīng)方程:
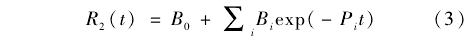
式中:t為時(shí)間;Pi為方程式的極點(diǎn);B0,、Bi為常數(shù).
由于LCSR響應(yīng)方程的極點(diǎn)與插入試驗(yàn)響應(yīng)方程的極點(diǎn)一致,因而可計(jì)算出熱電偶插入試驗(yàn)的響應(yīng)方程:
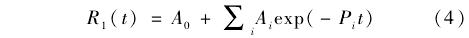
式中:A0、Ai為常數(shù),。
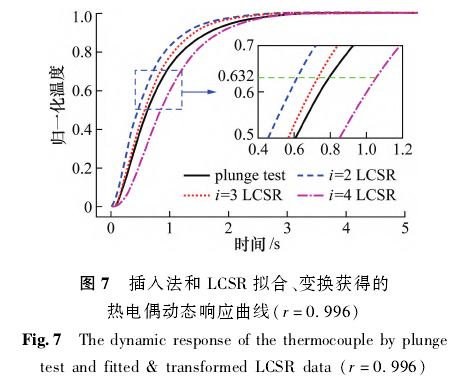
圖7所示為r=0.996時(shí),,插人法和LCSR擬合、變換(i=2,3,4)獲得的熱電偶動(dòng)態(tài)響應(yīng)曲線,。i=3時(shí),LCSR擬合,、變換得到的熱電偶對(duì)周圍流體溫度階躍變化的響應(yīng)曲線與插人法得到的響應(yīng)曲線最接近,局部放大圖上顯示時(shí)間常數(shù)也與插人法得到的時(shí)間常數(shù)最接近,。這是由于當(dāng)i=2時(shí),擬合公式的項(xiàng)數(shù)較少,導(dǎo)致擬合,、變換的誤差較大;當(dāng)i=4時(shí),原始數(shù)據(jù)的噪聲被放大,導(dǎo)致擬合,、變換的誤差增大,這與Rupnik等的結(jié)論一致。
絕緣層MgO填充密實(shí)度r對(duì)熱電偶時(shí)間常數(shù)?的影響如圖8所示,。隨著r增大,,絕緣層的熱導(dǎo)率增大,導(dǎo)致熱電偶的響應(yīng)速度加快、時(shí)間常數(shù)減小,。

不同r時(shí),,用式(3)和式(4)在i=2,3,4下擬合、變換LCSR響應(yīng)方程,獲得對(duì)應(yīng)插人法的響應(yīng)方程,求取時(shí)間常數(shù),。在i=3時(shí)求得的時(shí)間常數(shù)與插人法獲得的時(shí)間常數(shù)最接近,且偏差小于10%結(jié)果說明可以通過數(shù)值仿真的方法對(duì)熱電偶的動(dòng)態(tài)響應(yīng)過程進(jìn)行分析,結(jié)果偏差滿足應(yīng)用要求,。
6結(jié)論
采用有限體積法對(duì)鎧裝熱電偶的動(dòng)態(tài)響應(yīng)過程.進(jìn)行了數(shù)值仿真,建立了熱電偶保護(hù)管、絕緣層,、感溫層的三維模型,分析了網(wǎng)格劃分尺寸對(duì)仿真結(jié)果的影響,。在不同絕緣層MgO填充密實(shí)度下,分析了插人法和LCSR法獲得的熱電偶動(dòng)態(tài)響應(yīng)曲線,對(duì)LCSR響應(yīng)數(shù)據(jù)進(jìn)行擬合、變換,結(jié)果表明,隨著填充密實(shí)度增大,絕緣層的熱導(dǎo)率增大,,熱電偶的響應(yīng)速度加快,時(shí)間常數(shù)減小,。采用3個(gè)極點(diǎn)的響應(yīng)方程對(duì)LCSR響應(yīng)數(shù)據(jù)進(jìn)行擬合、變換求得的時(shí)間常數(shù)與插人法獲得的時(shí)間常數(shù)偏差小于10%,說明可以通過數(shù)值仿真的方法對(duì)鎧裝熱電偶的動(dòng)態(tài)響應(yīng)過程進(jìn)行分析,為快響應(yīng)熱電偶動(dòng)態(tài)特性的設(shè)計(jì)校準(zhǔn)提供了一種新方法,。